PROGRAMMING IN ATLAS AUTOCODE COMPUTER UNIT REPORT No. 1 by P.D. Schofield and M.R. Osborne (Revised Edition) 28th June 1965
These diagrams are stored as monochrome PNG files, and the non-ASCII characters are represented using the following HTML entities: ² for squared, ½ for half, α for alpha, π for pi, ≠ for inequality, ≤ for less than or equals, ≥ for greater than or equals, ↑ for exponentiation, √ for square root. Superscripts are represented using HTML's <sup>.
A handful of overprinted characters need to use Unicode combining characters.
These are used to represent character literals in Autocode,
see the Atlas Autocode manual for further details.
However, most browsers on most OSes don't display these correctly,
so we use strikeouts instead. The characters are s, n and semicolon, and should
in reality have either a slash or vertical bar through them as follows:
"s", "n", ";",
"s", "n", ";".
PROGRAMMING IN ATLAS AUTOCODE COMPUTER UNIT REPORT No. 1 by P.D. Schofield and M.R. Osborne (Revised Edition) 28th June 1965
(i)
PREFACE
This is a revised version of Computer Unit Report No. 1,
which was originally issued on 3rd, Mar. 1964. The revision was
undertaken not only to improve the text, but also to take account of
such changing circumstances as
(i) Changes in the compilers available on Atlas,
(ii) The writing of the Edinburgh University Atlas Autocode
compiler which has made Atlas Autocode available also on the K.D.F.9.
This book is intended to serve as an introduction to the
Atlas Autocode programming language. It is based on courses of
lectures given at Edinburgh University, and describes a version of
the language acceptable to all current Atlas Autocode compilers.
For a complete beginner, the following should prove
suitable for a first reading:-
Chapters 1 - 5 (But see note on page 27 and omit any
parts of pages 40, 48 which cause the
reader trouble).
Chapter 8 (pages 89-91. These may be read any
time after page 44).
We should point out that our examples are chosen to
illustrate points of the language: we do not claim that the
techniques used are in any sense the best possible.
We should be glad to hear from anyone who discovers or
suspects any errors.
In making this revision, we have benefited considerably
from discussions with our colleague Mr. Harry Whitfield, who
led the team writing the Edinburgh University compiler.
Our thanks are due to Mrs. Jackie Snashall and Miss
Isabel Fraser who bore the burden of re-typing and to Mr. Brian Read
who compiled the index and produced some of the diagrams.

(ii)
(iii) TABLE OF CONTENTS pages CHAPTER 1 : INTRODUCTION 1 - 12 CHAPTER 2 : BASIC NUMERICAL OPERATIONS 13 - 26 CHAPTER 3 : BASIC SYMBOL OPERATIONS 27 - 34 CHAPTER 4 : EXPRESSIONS, CYCLES, FURTHER ARRAYS 35 - 52 CHAPTER 5 : BLOCK STRUCTURE 53 - 60 CHAPTER 6 : ROUTINES AND FUNCTIONS 61 - 72 CHAPTER 7 : MORE ADVANCED FACILITIES 73 - 82 CHAPTER 8 : GENERAL TOPICS 83 - 91 INDEX : 93
(iv)
2.
3.
PROGRAMMING IN ATLAS AUTOCODE
This book is intended for those who wish to learn to write programs
in Atlas Autocode, a language available on both Atlas and KDF9 computers.
A program consists of a detailed set of instructions to the computer,
explaining exactly hew it is to solve a certain problem. It therefore
follows that the programmer must first:-
(a) Formulate the problem and decide on the method to be used to
obtain a solution. Only then can he
(b) Write a program describing the method already chosen.
Although this book is mostly devoted to describing process (b), it
must be emphasised that, in any moderately large problem, it is
process (a) which contributes most to the success or failure of a
project.
Two general suggestions can be made about this planning stage.
Firstly it often pays to draw a 'flow diagram' to help plan the logical
connections between different parts of the program. The reader will
find many examples of flow diagrams in the subsequent pages. Secondly,
considerable effort and money can often be saved by seeking, at the
earliest possible stage, the advice of someone who has successfully
completed a similar project.
Figure 1 uses the formalism of a flow diagram to indicate the steps
involved in using a computer to solve a problem.
5.
THE COMPUTER
The basic operation of the computer is most easily
understood from the following simplified (and partly fictitious)
diagram:-
Fig. 2
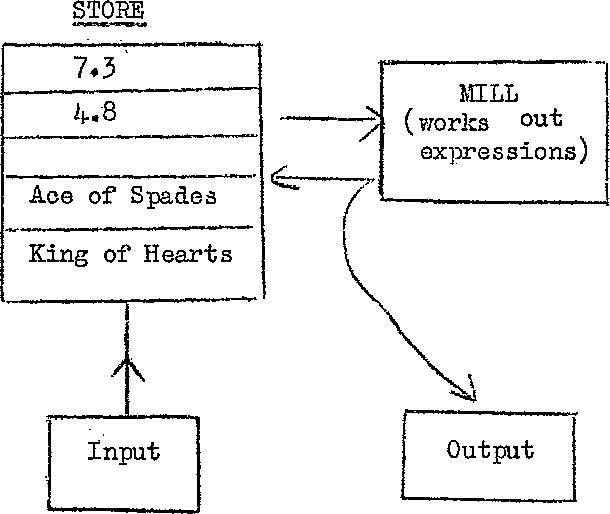 The STORE consists of a large number of locations in which
information can be deposited. Depending upon the way in which the
machine is being used, this information may be thought of as numbers,
values of playing cards; letters etc. Some of the store also contains
instructions which tell the computer what to do next.
The MILL is a place into which the machine copies pieces of
information from the store and works out expressions depending upon this
information.
e.g. (1) copy the first two numbers from the store and multiply them.
(2) copy the two cards in locations 4 and 5, and find the
higher-ranking.
When an expression has been worked out, it can either be printed out
as an answer, or replaced in the store for use later.
The STORE consists of a large number of locations in which
information can be deposited. Depending upon the way in which the
machine is being used, this information may be thought of as numbers,
values of playing cards; letters etc. Some of the store also contains
instructions which tell the computer what to do next.
The MILL is a place into which the machine copies pieces of
information from the store and works out expressions depending upon this
information.
e.g. (1) copy the first two numbers from the store and multiply them.
(2) copy the two cards in locations 4 and 5, and find the
higher-ranking.
When an expression has been worked out, it can either be printed out
as an answer, or replaced in the store for use later.
6.
Moving information in or out of a location in the store is in
some ways similar to the operation of a tape recorder. When withdrawing
information ('reading'), we take a copy of the contents of the location.
The original information is still there, and can be used again as often
as required. When putting information in ('writing') the previous contents
of that location are destroyed.
Warning : If we road the contents of a location before putting anything
in, we are in danger of obtaining whatever was left behind at the end of
the previous program.
INPUT
When we wish to use the computer, we normally need to feed in
two 'documents' (1) Program
(2) Data
The difference between the two is shown by the two examples below:-
Program Data
Method for solving a set of equations Set of equations
Method for sorting words into dictionary order List of words
Most of the program consists of a series of instructions telling
the computer to carry out various operations. These are kept in the store
in a code or 'language' which is not readily comprehensible to the programmer.
It is possible, but tedious, to write programs in this language (in the
early days of computers, nothing else was available). Nowadays we can
write in a more convenient language, Atlas Autocode for example, and the
computer is supplied with a COMPILER which translates the program into its
own language.
In the first place the program, and often the data as well, will be
written down with pencil and paper. After careful checking, this will be
converted into suitable form (normally punched paper tape or punched cards)
for feeding to an INPUT device.
7.
OUTPUT
The results of the calculation will come out via an OUTPUT device
which either prints out answers directly, or produces punched paper
tape or cards for subsequent printing. A device for printing out
answers directly is known as a LINE PRINTER.
We can now give an improved version of Fig. 2:-
Fig. 3

8.
The sequence of events should be:-
(1) Read in Program.
(2) Compile (i.e. translate) into machine instructions.
(3) Execute the compiled program which will contain instructions to
(a) Road in Data
(b) Carry out Calculation/Processing
(c) Print out Results
However if any violations of the rules of the language are detected
during the compiling stage, no attempt is made to execute the program,
but instead a list of faults is printed out.
Even after execution of the program has started, some part of the
translated program may turn out to be impossible for the machine to
execute. For example, it cannot divide by zero. The execution will
then cease and an appropriate fault signal will be printed.
9.
ORDER OF PRESENTATION TO COMPUTER
In a small job, the preliminary information (Job Heading), program
and data are usually all supplied to the computer on one piece of tape ordered as follows:-
*** A ) Job Heading giving title of program
JOB ) and stating which compiler is to
BLOGGS' FIRST PROGRAM ) be used to translate the program
COMPILER AA ) following. (AA=Atlas Autocode)
begin )
..... )
..... )
..... ) Program
..... )
..... )
end of program )
..... )
..... )
..... ) Data
..... )
..... )
*** Z ) Marks end of tape
NOTES
(1) Programs written in Atlas Autocode can at present be run on either
an Atlas or a KDF9 computer. If using an Atlas, we have the choice of
two compilers, both written at Manchester University
(a) COMPILER AA
(b) COMPILER AB
The latter is a faster but somewhat restricted version of AA.
The Atlas Autocode compiler for KDF9 has been written at Edinburgh
University.
Except where specially indicated, this book describes how to
write programs equally acceptable to all three compilers. Precise
specifications of each compiler can be obtained from the appropriate
Computer Unit.
(2) The example of a Job Heading given above is the minimum required.
New programmers should consult the Computer Unit of their own University
to discover what extra details need be given in any particular case.
10.
ANALYSIS OF A VERY SIMPLE PROBLEM
Suppose that we wish to read in a string of letters of the
alphabet (in any order) and count hew many times each letter occurs.
To mark the end of the string we shall use a full stop.
A convenient method of doing this is to set up 26 counters in
the machine, one for each letter of the alphabet.

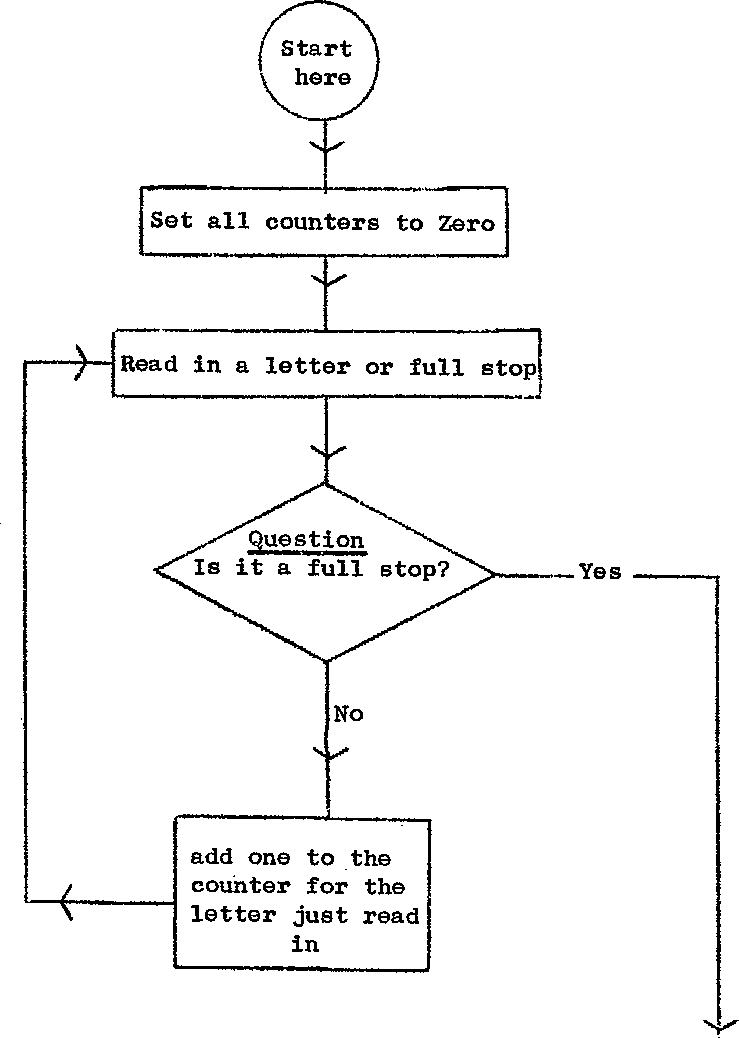
11.
Suppose we now wish to print out the number of times each letter
has occurred. The process is:-
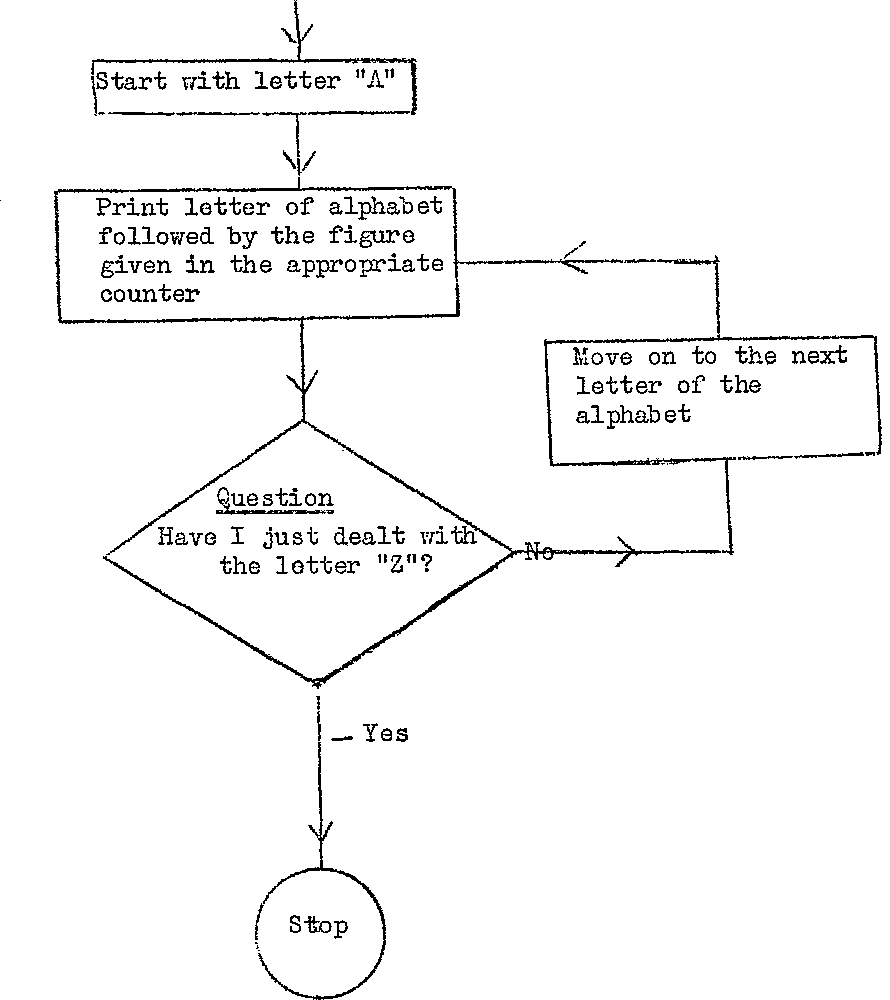
12.
14.
15.
ATLAS AUTOCODE
The Atlas Autocode language is better equipped for dealing
with numbers than with other types of information. For this reason,
the basic principles of the language will first be explained in terms of very
elementary calculations with numbers. Some equivalent orders for
manipulating non - numerical symbols will be given in Chapter 3.
NAMES
Before a number or symbol can be placed in a location of the store, this
location must be given a name. A name must start with a letter and consist
of
(a) one or more letters (a,b,.....z,A, B, ... Z)
(b) possibly followed by one or more digits (0, 1, 2, ... 9)
(c) possibly followed by one or more primes (', '', ''' etc.)
Examples x, a2'', total 3, SUM', Sum
Notes (1) a2c is not permitted as a letter follows a digit.
(2) The compiler completely disregards all spaces (and underlined
spaces) in the program. Spaces may thus be used to improve
legibility of program.
LINES
The basic units of a program are
(a) Declarations
(b) Instructions
(c) Separators
These will be described in the following pages. We shall refer to them
collectively as 'lines', since they are normally written on distinct lines.**
However, two or more 'lines' can be written on the same physical line, provided
they are separated by semi-colons.
** What is here called a 'line' is often called a 'source statement' in
the literature.
16.
DECLARATIONS
Names are allocated to locations in the store by means of
declarations such as:-
Declaration Meaning
real a set aside the next unused location, call it
a and be prepared to put a 'real'
number in it later.
integer b, c3 set aside the next two unused locations,
call them b and c3 and be prepared to
put integers (whole numbers) in them later.
Note (1) Generally speaking, a name allocated to a location will remain
fixed throughout the program. However, the contents will vary whenever
new number is placed in it.
(2) The word 'variable' is used to describe locations which, have been
set aside to contain numbers, either real or integer.
(3) There are three distinctions between real variables and integer
variables:-
(a) An integer variable can only contain a whole number. A real
variable may contain either an integer or a number such as 73.4827, with up
to 11 significant figures.
(b) There are certain purposes for which only integer variables
are allowed. (e.g. To give the number of times a group of instructions
is to be repeated: repeating 1.7 times would be impossible).
(c) When we do multiplications and additions of integer variables, the
machine produces the exact answer. When doing arithmetic on real variables,
the answers are 'rounded off' to 11 significant figures.
UNDERLINING
Note that the underlining of certain key words (real and integer above,
for example) is an integral part of the language. At this stage the
reader is advised to accept, as arbitrary rules, that certain words are,
and others are not underlined.
17.
DECLARATION OF ARRAYS
We can also declare a whole array of variables, all having the same
name, but distinguished from one another by means of a 'suffix' in brackets
after it,
real array d(1:4) set aside 4 locations :- 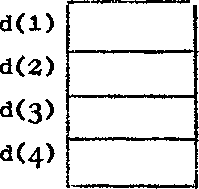 real array e(1:7),f,g (0:4) set aside ( 7 locations for e(1) to e (7)
(
( 5 locations for f(0) to f (4)
(
( 5 locations for g(0) to g (4)
Notes (1) Arrays of integer locations are declared in a similar manner by
writing integer array ........
(2) In the case of real arrays, it is permissible to omit the word
real, simply writing array ........
(3) Note the difference between
real array d(1:4) which gives four locations
and real d4 which gives only one location
These four types of declaration are normally written on separate lines,
but may instead be separated by a semi-colon.
either real a,b,x3'
integer array y (1:20)
or real a,b,x3' ; integer array y (1:20)
Further types of declaration, allocating names to functions, routines,
switches, and multi-suffix arrays will be described later. Declarations are
preparatory in nature, and should be contrasted with 'instructions' which,
when executed, bring about the transfer of information to locations already
prepared.
Note : A name cannot be used simultaneously for two different purposes.
For example:-
real A
real array A(1:10)
would cause a fault signal.
real array e(1:7),f,g (0:4) set aside ( 7 locations for e(1) to e (7)
(
( 5 locations for f(0) to f (4)
(
( 5 locations for g(0) to g (4)
Notes (1) Arrays of integer locations are declared in a similar manner by
writing integer array ........
(2) In the case of real arrays, it is permissible to omit the word
real, simply writing array ........
(3) Note the difference between
real array d(1:4) which gives four locations
and real d4 which gives only one location
These four types of declaration are normally written on separate lines,
but may instead be separated by a semi-colon.
either real a,b,x3'
integer array y (1:20)
or real a,b,x3' ; integer array y (1:20)
Further types of declaration, allocating names to functions, routines,
switches, and multi-suffix arrays will be described later. Declarations are
preparatory in nature, and should be contrasted with 'instructions' which,
when executed, bring about the transfer of information to locations already
prepared.
Note : A name cannot be used simultaneously for two different purposes.
For example:-
real A
real array A(1:10)
would cause a fault signal.
18.
INSTRUCTIONS
Some simple types are given below. They are written on separate lines
or separated by semi-colons in the same manner as declarations.
Input Instructions (also see p. 85) Meaning
read (a) read in the next number in the data and
put it in the location whose name is a.
read (b, c3,.d(4)) read in the next 3 numbers in the data
and put them in b, c3, and d(4)
Assignment instructions (also see p. 42)
These look like mathematical equations but the meaning is quite
different.
Instruction Meaning
a = b + c work out the expression on the right
(i.e. contents of b plus contents of
c) and then put it in the location
given on the left (i.e. a)
Thus
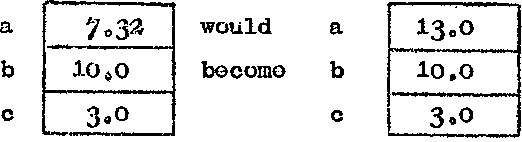 a = 2a + 1 copy the contents of a, double it, add
1 and place the answer back in a.
Notes (1) b + c = a is not permitted since b c is not the name of a variable.
(2) a = b - is quite different from b = a.
(3) the use of more complicated expressions on the right will be
explained later.
a = 2a + 1 copy the contents of a, double it, add
1 and place the answer back in a.
Notes (1) b + c = a is not permitted since b c is not the name of a variable.
(2) a = b - is quite different from b = a.
(3) the use of more complicated expressions on the right will be
explained later.
19.
Output Instructions (Also see p. 86)
print (x, 3, 1) work out in the Mill the value of the
print (2x + y + 7, 3, 1) - first expression in the brackets (i.e.
x or 2x + y + 7) and print the value
of the expression with 3 figures
before the decimal point and one after.
(The figures 3 and 1 can, of course,
be varied).
newline output printer is to go to the start
of a fresh line, moving the paper up
accordingly.
newlines (2) equivalent to:- newline ; newline
space output printer is to leave one blank
space (printing takes place from
left to right across the page)
spaces (3) equivalent to:- space; space; space
caption MORRIS1100 output printer is to print out the
set of characters MORRIS1100.
Note The instruction caption ..... is chiefly used to obtain headings
and explanatory notes in the output. These notes may be required to
include spaces, newlines, etc.
A special method is provided for outputting the symbols space,
newline and semi-colon with a caption, since spaces are ignored by the
computer and a semi-colon or newline character marks the end of the
caption 'line':-
s or s represents a space
n or n represents a newline
; or ; represents a semi-colon,
Either
(a) caption n MORRIS ss 1100
or (b) newline ; caption MORRIS ; spaces (2) ; caption 1100
will produce an output (at the beginning of a newline):-
MORRIS 1100
20.
SEPARATORS
A few lines, neither declarations nor instructions, have to be written
into a program, chiefly to mark the begining and end of blocks and
routines. Examples are begin end and end of program, described on the
next page.
COMMENTS
Any line starting with comment is disregarded by the compiler. This
permits the insertion of explanatory notes, which must not contain a
semi-colon, for the benefit of the reader. For example:-
read (n)
comment n is the number of cases to be solved.
For brevity, a single vertical bar can replace comment. For example:-
read (n)
| n is the number of cases to be solved.
A third equivalent method of writing the above is:-
read (n) ; | n is the number of cases to be solved.
21.
BLOCKS
A program is normally split up into a number of blocks. In general a
block consists of
begin
...... )
)
...... )
)
...... ) declarations
)
...... )
)
...... )
...... )
)
...... )
) instructions
...... )
)
...... )
end
At the end of the last block of a program, end is replaced by
end of program.
Example begin
real array a(1:3)
real b
read (a(1),a(2),a(3))
b = a(1)+a(2)+a(3)
print (b,2,3)
end of program
This causes the machine to read in three numbers, add them and print out
the total.
Note The machine automatically terminates the calculation on reaching
end of program. If it is required to stop the calculation at any other point,
the instruction stop is used.
22.
LABELS
Any 'line' in the program can be labelled by writing on the left
a positive integer, followed by a colon. The label has no effect other
than to give the line a reference number.
EXAMPLE
i=i+j
10: read (x)
x=x+i
JUMP INSTRUCTIONS
Normally, instructions are obeyed in the order in which they are
written. In order to make the machine jump, either forwards or
backwards, to a labelled line in the program we can use a jump
instruction written, for example:-
instruction meaning
-> 10 the next line to be
obeyed is the one
labelled 10:
Notes (1) By making the machine jump back to an earlier part of
the program we can make it go round a loop of instructions many times.
(2) Although jumps can be either forwards or backwards, we
are not allowed to jump from one block to another.
(3) Jump instructions are frequently made conditional, as
described in the next section.
23.
CONDITIONAL INSTRUCTIONS
Assignment and jump instructions may be made subject to a condition.
Examples Meaning
a = b + c if x = 0 Carry out the instruction if
-> 27 unless a > b + 2 (or unless) the condition is
stop if n>100 satisfied. Otherwise skip and
pass on to the next instruction.
If preferred, instructions may be written with the condition first,
followed by then:
if x = 0 then a = b + c
unless a > b + 2 then -> 27
if n > 100 then stop
Note (1) Note the different uses of '=' in the first example. In x = 0
it has its normal mathematical significance. In a = b + c it means an
assignment.
(2) In the condition we may use any of the relations = ≠ > ≥ < ≤
MORE COMPLICATED CONDITIONS
These may be formed
(1) with a two-sided condition **
e.g. if 0 < x < 1 + y then .......
(2) by writing several conditions separated by and with the obvious
significance.
e.g. if x>0 and y = 0 and z ≠ 2 then ........
(3) by a similar use of a succession of or's
e.g. if x>0 or y = 0 or z ≠ 2 then .........
(4) by combining (2) and (3) provided and's or or's are separated by
brackets.
e.g. if (x>0 or y = 0) and z ≠ 2 then ..........
** This form of condition is not accepted by the Manchester Compiler AB.
24.
EXAMPLE OF A SIMPLE PROGRAM
Suppose we want to road in a list of positive numbers and print
out their average. Suppose we do not know in advance how many there will
be. In order to inform the computer when we have come to the end of
the list, we terminate it with the number -1.
We shall need the following variables:-
(1) a place in which to put the numbers as they are read in.
(2) a running total.
(3) a count (integer n, say) of how many numbers have boon read in.
Note that (2) and (3) must be set to zero before starting.
A possible flow diagram is given on the next page:-
25. PROGRAM FOR PRINTING AVERAGE A possible flow diagram is:and a program to implement this is:- begin integer n real total, x n = 0; total = 0 10: read (x) -> 11 if x = -1 total = total + x n = n + 1 -> 10 11: newline caption Average s = print (total/n,3,5) end of program
26.
28.
29.
MANIPULATION OF SYMBOLS
INTEGER variables can not only be used to store integer NUMBERS as
described in the last chapter, but can also hold SYMBOLS. Possible symbols
include
(a) The letters of the alphabet (both upper and lower case),
(b) The numerical digits 0 to 9 (see note 1 below).
(c) ( ) [ ] . , : ; ' ?
(d) + - * / ↑ | = ≠ > ≥ < ≤ α π
(e) space and newline.
Notes
(1) The symbol 9 is NOT the same as the number 9.
(2) Symbols can be stored in integer variables, including elements of
integer arrays.
INPUT OF SYMBOLS (See also p. 87)
Input Instruction Meaning
read symbol (a) Road the next symbol on the data tape
and place it in location a. Move the
data tape on by one symbol,
Note (1) The instruction read symbol
can only road one symbol at a time
(unlike the instruction read which may
read several numbers).
Note (2) a MUST be an integer variable
or an element of an integer array.
Important Note When reading numerical data, spaces and newlines simply
mark the end of a number. However, both spaces and newlines count as
symbols and will be road in by the routine read symbol.
30.
ASSIGNMENT OF SYMBOLS
Instructions to assign symbols to integer variables are written in
a form very similar to those which assign numbers, but the symbol
concerned is written between a pair of 'quotation marks'. For example:-
integer i, j, k
i = '*'
j = 'P'
k = '7'
Note that the last two instructions assign the SYMBOLS P and 7 to j and k
respectively. On the other hand, the instructions
j = P
k = 7
assign to j the NUMERICAL value currently stored in the variable named P,
and to k the NUMBER 7.
CONDITIONS
Conditions depending upon the equality, inequality, etc. of symbols
may be written in a fairly self-evident manner e.g.
if i = '*' then stop
-> 9 unless k = '?' or j = 'A'
31.
SYMBOLS FOR SPACE, NEWLINE
It was explained on page 19 why it is necessary to write spaces,
newlines, etc. in a special manner within a caption. The same problem
arises when we wish to write these SYMBOLS in assignment instructions,
conditions, etc. and the same special conventions are used. For example,
i = 's'
assigns the symbol 'space' to the variable i.
A simple method of reading the next 'useful' symbol in data
(i.e. disregarding spaces and newlines) would be:-
integer i
1: read symbol (i)
-> 1 if = 's' or i = 'n'
............
............
OUTPUT OF SYMBOLS
The instructions
( caption ............. )
( space )
( spaces ( ) )
( newline )
( newlines ( ) )
are available for output of symbols, as described on page 19. There
is also an instruction print symbol:-
Instruction Meaning
print symbol ('*') print out the symbol *
print symbol (i) print out the symbol currently held
in the integer i
Note (1) The first instruction above could equally well be written:-
caption *
(2) print symbol (i) is useful when we do not know in advance what
symbol is going to be stored in the integer i.
32.
RELATIONSHIP BETWEEN SYMBOLS AND INTEGERS
Symbols are stored in integer variables, and in fact each symbol
has a numerical value to which it corresponds. However, since this
correspondence may vary between compilers, programmers are advised not
to make use of this fact. On the other hand, all the compilers are
arranged so that 'A' has a value one less than 'B', which is one less
than 'C', etc., thus preserving the natural dictionary ordering. The
same is true of 'a', 'b',..... etc. and of '0', '1'..... etc.
Example
To test whether the next symbol on the data tape is a lower case
letter in the first half of the alphabet we could write:-
read symbol (i)
if 'a' ≤ i ≤ 'm' then ...............
33.
EXAMPLE OF A PROGRAM TO COUNT SYMBOLS
Suppose that we wish to road in a sequence of symbols as far
as the first full stop, and print out the percentage which are capital
E's. The program required is almost identical to that used on page 25
to print the average of a list of numbers,
begin ; comment to give percentage occurrence of letter E
integer n, Number of Es, x
n=0 ; Number of Es = 0
10: read symbol(x)
->11 if x = '.'
if k = 'E' then Number of Es = Number of Es + 1
n = n +1
-> 10
11: newline
caption percentage s of s E's s =
print(100*Number of Es/n,2,1)
end of program
For comparison purposes, the program from page 25 is
reprinted below:-
begin ; comment to give average of a list of numbers
integer n
real total, x
n = 0 ; total = 0
10: read (x)
-> 11 if x = -1
total = total + x
n = n + 1
-> 10
11: newline
caption Average s =
print (total/n,3,5)
end of program
34.
36.
37.
ARITHMETIC EXPRESSIONS
There are many places in a program where we have to write
an arithmetic expression (e.g. on the right of an assignment instruction
or in a print instruction). The simplest form of expression is a single
variable or numerical constant. More generally, an expression consists
of variables, constants and functions, connected together by
mathematical symbols. The method of writing constants is given below;
variables have already been described - (pages 16 - 18) and functions will
be deferred until page 40.
constant meaning note
37 ) obvious 0.25 and .25 are
0.25 ) equally valid.
2.374 )
1α3 1000(i.e. 1 x 103 ) (i) This is called the
'floating point' form
1.732α-2 0.01732 for a constant,
(i.e. 1.732 x 10-2) (ii)The number after α
must be an integer
constant.
π 3.14159....
½ 0.5 ½ is one symbol.
Other fractions must
be written as
quotients(i.e. 1/3)
38.
Mathematical Symbol Meaning
+ addition
- subtraction
* multiplication
/ division
↑ raise to a power (a↑3 means a3)
² squaring
| used in pairs as modulus signs.
Notes
(1) In normal mathematical notation we often omit the multiplication
sign (e.g. ab for a*b). In Atlas Autocode we write the * sign,
otherwise the compiler will look for a variable with the name 'ab'. The
* can be omitted where a constant is followed by a variable
(e.g. 3.5*y and 3.5y are equivalent)
(2) a² and a↑2 are equivalent. All other powers must be written with ↑.
(3) In manuscript, the symbol ↑ is usually written ↑.
39.
PRECEDENCE OF OPERATORS (+ - * / ↑)
There may be some uncertainty about the meaning of an expression such
as a*b+c. Do we carry out the multiplication first, giving (a*b)+c, or
the addition first giving a*(b+c) ?
In the absence of brackets, we have the rule that, of two adjacent
operators (like * and + above), the operator of higher precedence in the
table below is to be carried out first.
(1) ↑ (highest precedence)
(2) * or /
(3) + or - (equal lowest precedence)
Where two adjacent operators are of equal precedence by the above table,
the one appearing to the left (in the expression to be evaluated) is carried
out first.
Notes (1) The multiplication operator between a constant and a variable has
the same precedence whether written explicitly or 'implied' (see note 1 on
previous page)
(2) The symbol ² is treated as equivalent to the pair of symbols ↑ 2
and precedence is given accordingly.
(3) If we wish to over-ride the above rules, we must use brackets as
in normal mathematical notation.
(4) When in doubt it is wisp to insert brackets for safety and
clarity.
(5) The 'left-hand precedence' between + and - agrees with normal
usage.
e.g. By a-b+c we mean (a-b)+c and not a-(b+c)
Examples Meaning
a/b*c a x c
b
a/(b*c) a
bc
a↑(b*c) abc
Note The first two examples show that it is necessary to bracket
denominators containing more than one term. A common mistake is to write
a/2b when a/(2b) is intended.
40.
FUNCTIONS
In addition to variables and constants, functions may also be included
within expressions. The basic functions available are:-
real function meaning note
sin(x) ) as in
cos(x) ) elementary x in radians
tan(x) ) trigonometry
sq rt (x) +√x
log (x) logarithm of x to base e
exp (x) ex
mod(x) modulus of x mod(-3.7)=3.7;mod(3.7)=3.7
(i.e. Absolute Can be written |x|, but
value of x) see note below.
arctan (x,y) tan-1 (y/x) In radians. Value is in
1st or 4th quadrant if x>0
2nd or 3rd quadrant if x<0
radius (x,y) +√x²+y²
frac pt (x) fractional part of x frac pt(3.73)=0.73
frac pt (-3.73)=0.27
integer function meaning note
int(x) nearest integer to x int (3.73)=4
int pt (x) integral part of x int pt (3.73)=3
int pt (-3.73)=-4
parity (n) +1 if n is even n must be an
-1 if n is odd integer variable.
Notes (1) The first group of functions (down to frac pt) all produce
a number of type real, which can only be assigned to a real variable. The
last three produce a number of type integer.
(2) In particular, note that the function mod(x) produces a number
of type real, irrespective of whether x is of type real or integer. On the
other hand, a pair of modulus signs will give the same numerical value as the
modulus function, without altering the type, (i.e. integer remains integer).
Hence, if n is an integer,
n = |n| is valid
n = mod(n) will be faulted.
(3) The above functions are all understood by the compiler before
the program is read in. The method used to define additional functions, if
required, will be given later (page. 70)
(4) As the names sin, log etc. are already in use, they should
not be used by the programmer in any of his declarations.
41.
INTEGER AND REAL EXPRESSIONS
The differences between integer expressions and real expressions lie not
so much in the values of the expressions as in how they are constructed and
used.
(1) Any expression consisting entirely of integer variables, integer
constants and integer functions is called an INTEGER EXPRESSION. Any
other expression is called a REAL EXPRESSION.
(2) We shall meet a number of places where an integer expression is
required. In these cases, a real expression is not allowed, not even one
whose value may actually work out to be an integer. On the other hand,
wherever a real expression is expected, an integer expression will do instead.
Integer Expressions
The main cases where an integer expression is compulsary are:-
(1) When assigning a value to an integer variable.
(2) As the suffix of an array element.
(3) As the power to which a number is to be raised. (Raising to a power
is done by repeated multiplication).
(4) In cycle instructions (page 43)
Examples Suppose we have declared
integer i
real x,y
real array d(0:10)
Example of (1) Although x=i is permitted, i=x will cause a fault signal
because x is a real expression.
Example of (2) If we have previously set i=3; x=3 then d(i*i) refers to d(9)
but d(i*x) is illegal.
Example of (3) x↑3 and x↑(i+1) are legal expressions but x↑y is not.
Symbols as Integer Expressions
A symbol written between 'quotation marks' is a possible form of integer
expression, but should only be used with caution. A simple and safe
example of this will be found on Page 47.
42.
FURTHER ASSIGNMENT INSTRUCTIONS
The general form of an assignment is either
(1) assign the value of an INTEGER expression to an INTEGER variable or
(2) assign the value of a REAL or INTEGER expression to a REAL variable.
Examples Suppose we have declared real a,b,c,x
integer i,j,k
then possible instructions are:-
x = (-b + sq rt (b*b - 4a*c))/(2a)
i = int(j/k) + j*j
a = log (1 + cos (2! x)) 3.74b
x = i
Notes (1) As already explained i = x will cause a fault signal because
x is real. If required, we can write: i = int(x)
(2) On the Atlas versions of the language we can, without a fault
signal, assign to an integer variable any integer expression. The
responsiblilty for ensuring that the expression will work out to be
an integer, lies with the programmer. (division or raising to a negative
power are possible causes of non-integer results). See the second example
above.
(3) When using KDF9 there is the further restriction that,
whenever an integer expression is compulsary, each stage in the evaluation
of the expression must yield an integer result. Referring to the rules of
precedence for operators, we see that, with the previous declarations,
j = i*(i+1)/2 will always work but that
j = (1+1)/2*i while having the same result as the previous line
when- (141) is even, will be faulted if (i+1) is odd.
(4) It is possible to use expressions inside larger expressions;
in particular we can have a function of a function as in the third example.
43.
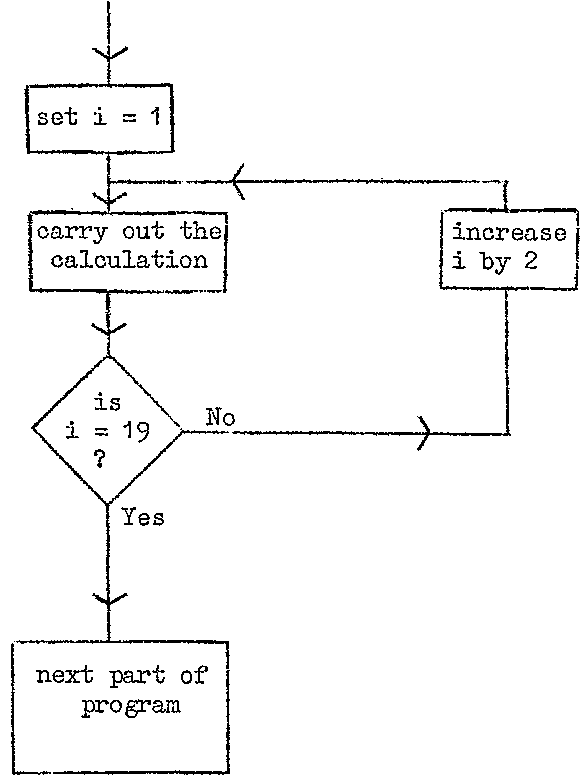
CYCLES
Suppose that we wish to carry out a certain part of a program
10 times with an integer i taking the values 1,3,5.........,19 on
successive occasions.
Clearly it is necessary to indicate
(1) the sequence of values which the integer is to assume, and
(2) the beginning and end of that section of program which is
to be repeated.
We achieve this by writing:-
cycle i = 1,2,19
( orders making )
( up the section )
( of program )
( to be repeated )
repeat
......
NOTES
(1) The sequence of values i is to assume is indicated by writing
'cycle i = ' followed by 3 integer expressions giving the initial
value, the increment, and the final value.
(2) The control variable i must have been previously declared to be
an integer or an element of an integer array.
(3) The separator repeat, is used to indicate the end of the section of
program to be repeated.
(4) The expressions for the initial and final values and the increment
are evaluated on first reaching the cycle. The number of times the cycle
is to be executed is
1 + (final value - initial value)/increment,
and a fault is signalled if this is not a positive integer.
44.
Instead of using cycle and repeat in the above example the same result
could have been obtained by using jump instructions. For example:-
i = 1
1: ( orders making )
( up section )
( of program )
( to be repeated )
-> 2 if i = 19
i = i + 2
-> 1
2: .......
The same flow diagram serves for both methods of writing this program:-
45.
NESTING OF CYCLES
Cycles may be nested to any depth. Each cycle must have exactly
one associated repeat.
Example
cycle i = 1,1,4
read (A(i))
newline
cycle j = 1,1,i
print (A(i)↑j,2,0)
spaces (2)
repeat ; comment this refers to cycle j =
repeat ; comment this refers to cycle i =
Supplied with the data
0 1 2 3
the output would be
0
1 1
2 4 8
3 9 27 81
NOTE
Within cycles, either single or nested, the control variable(s)
may be used for two distinct purposes:-
(a) to count the number of times the cycle has been executed, and
(b) to vary systematically quantities occurring in arithemetic expressions.
(e.g. the integer i in the above example both counts the number of times
the outer cycle is executed, and also enables us to operate on different
array elements on each occasion).
46.
Example
Use a cycle to simplify the program on pages 24-25 for
giving the average of a list of numbers.
Instead of using the special number -1 to terminate the data,
we head the list with an integer indicating how many numbers there are
to follow.
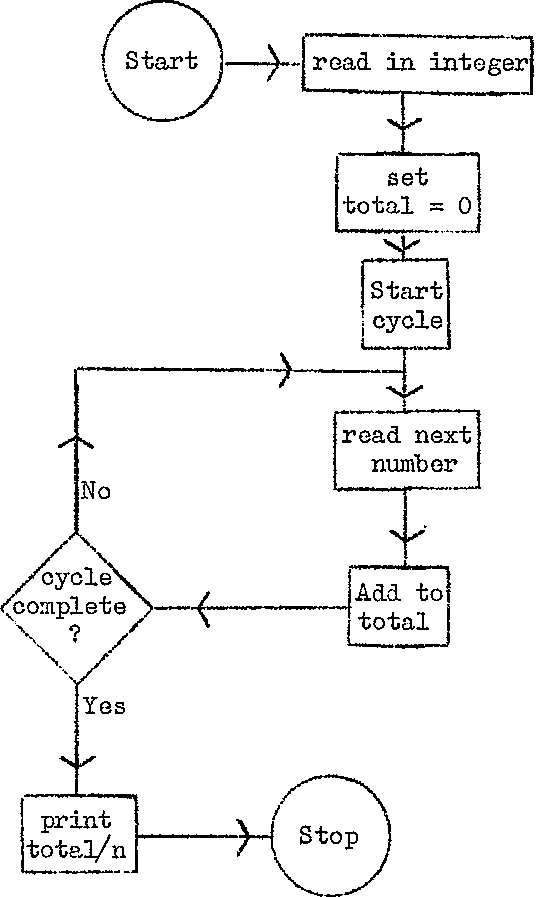
47.
EXAMPLE OF A CYCLE TO COUNT SYMBOLS
We can now program the flow diagram given at the end of the
introductory Chapter 1. The following program will only count capital
letters, and will disregard all other symbols except the terminating
full stop.
begin
integer array Counter ('A':'Z'); comment 'A' and 'Z' are integer constants
integer i, j
cycle i = 'A', 1,'Z'
Counter (i) = 0
repeat
1: read symbol (j)
-> 2 if j = '.'
Counter(j) = Counter(j) + 1 if 'A' ≤ j ≤ 'Z'; | disregard all other symbols
-> 1
2: cycle i = 'A',1,'Z'
newline
print symbol (i)
print (Counter (i),4,0)
repeat
end of program
48.
SWITCH LABELS
It is sometimes required to jump to one of several points
of a program, depending upon the value of some (integer) expression.
One method is given below on the left, with the equivalent and. more
compact use of a switch given on the right:-
switch A(0:3)
......
21: read (i) A(3): read (i)
-> 22 if i = 0 -> A(i)
-> 21 if i = 3
-> 23 if i = 2
22: a = b + c A(0): a = b + c
23: a = 2a A(2): a = 2a
NOTES
(1) As with ordinary labels, jumps can be either forwards or backwards,
but cannot go outside the current block.
(2) Switch declarations appear among the other declarations at the
head of the block, and hence the name is declared before being used
for either a label or a jump instruction.
(3) The name of the switch must not be used for any other purpose
at the same level.
(4) It is not necessary to use all the labels in the range declared
(note A(1) missing above), but a fault would be signalled if i had the
value 1 on reaching the instruction -> A(i).
(5) The bounds given when declaring a switch must be integer constants,
although the jump instruction can use integer expressions such as -> A(i+2j).
(6) The symbol -> can only be followed by a constant (ordinary label)
or an element of a switch.
49.
MULTI-SUFFIX ARRAYS
On page 17, we introduced declarations of arrays with one suffix. In a
similar manner we can declare arrays with two or more suffices.
declaration meaning
real array 1(1:2, 1:3) set aside 6 locations
for real variables to be
known as follows:
A(1,1)
A(1,2)
A(1,3)
A(2,1)
A(2,2)
A(2,3)
integer array A(1:2, 1:3) as above, but giving integer
variables.
Arrays with more than two suffices may be declared in a similar
fashion. For example:-
real array B(0:4, 0:4, 0:4)
integer array C(1:5, 1:5, 1:20, 1:30)
Example
Suppose we wish to form a table giving the number of successes in 'A'
level Mathematics, Physics, Latin and French, sub-divided into boys and
girls. Let us store the numbers in integer variables A(i,j) as follows:-
Maths Physics Latin French
Boys A(1,1) A(1,2) A(1,3) A(1,4)
Girls A(2,1) A(2,2) A(2,3) A(2,4)
Here the first suffix gives the sex and the second the subject.
To set all the first row to sere initially, we could write:
cycle j = 1,1,4
A(1,j) = 0
repeat
and then for the second row
cycle j = 1,1,4
A(2,j) = 0
repeat
50.
It is easier to combine these two processes by means of a cycle within
a cycle
cycle i = 1,1,2
cycle j = 1,1,4
A(i,j) = 0
repeat
repeat
The same method will be used to print out the results in a rectangular
table.
Data Suppose the data is supplied as follows:-
(1) An integer giving the number of results to analyse.
(2) Groups of three integers in which
the first indicates sex (1 for boy, 2 for girl)
the second indicates subject (1,2,3,4 as before)
the third indicates success (0 for fail, 1 for pass)
for example:-
data meaning
999 999 results to follow
1 A boy has taken Maths
1 and failed.
0
1 A boy has taken French
4 and passed.
1
2 A girl has taken Latin
3 and passed.
1
etc.
A possible flow diagram and program are given on the following
pages.
52.-
begin
integer i,j,k,l,n
integer array A(1:2: 1:4)
cycle i = 1,1,2
cycle j = 1,1,4
A(i,j) = 0
repeat
repeat
read (n)
cycle 1 1,1,n
read (i,j,k,)
if k = 1 then A(i,j) = A(i,j) + 1
repeat
newline
cycle i = 1,1,2
cycle j = 1,1,4
Print (A(i,j), 3,0)
spaces (5)
repeat
newline
repeat
end of program
Notes: (1) The inner cycles have been indented on the pages for clarity.
This is quite permissible as spaces in the program are disregarded by the
compiler.
(2) In order to achieve a rectangular layout of results, spaces
(5) are put in the inner cycle, and the newline in the outer cycle.
54.
55.
Block Structure
The basic layout of a block was described on page 21. It has
the form of begin followed by the appropriate declarations, then by
the instructions, and terminated by end. It is permissable to nest blocks
as in the following diagram
begin )
..... ) )
..... ) declarations )
..... ) )
)
)
)
..... ) )
..... ) )
..... ) ) outer block
) )
) )
) )
begin ) ) )
..... ) ) instructions )
..... ) inner block ) )
..... ) ) )
end ) ) )
) )
..... ) )
..... ) )
..... ) )
end )
Note (1) It is sometimes convenient to regard a whole block as one
compound instruction. With this view of the inner block, the outer block
has the structure given on page 21.
(2) Blocks may be nested within one another to any, depth.
(3) Blocks may not be made conditional.
Among the reasons for nesting blocks of program one inside another are the
following.
(a) It may be required to declare an array whose suffix bounds are not
known until some stage in the execution of the program. This is
illustrated in the following example where the first number read indicates
how many more are to follow
begin
integer n
read (n)
begin
real array A(1:n)
cycle i 1,1,n
read (A(i))
repeat
.....
end
.....
end
56.
(b) The declarations made at the head of a block are cancelled
on reaching the end which terminates the block. Thus if a program requires
large amounts of working space for each one of several distinct jobs,
then storage space can be economised if each job is written as a
distinct block. For example:-
begin
.....
.....
begin
real array A(1:10000)
..........
end
.....
.....
begin
real array B(1:20,1:500)
.............
end
......
.....
end
Note Storage limitations are particularly important on K.D.F.9 as none
of those supplied to the Universities can hold more than 16000 numbers
in the main store. The appropriate operating manual should be consulted
for further details.
(c) In developing a complicated program it is often a great advantage
that each sub-block can be developed seperately. A program is
generally much clearer if its sub-blocks are related to the blocks of
its flow diagram. Another and closely related method of breaking a
program down into sub-units is by the use of routines: see pages 63-69.
57.
LOCAL AND GLOBAL VARIABLES
It is important to appreciate the sphere of influence of the
declarations made in the inner and outer blocks.
A declaration appears at the head of a block and normally remains
valid throughout that block until cancelled by the end terminating the
block. It also remains in force upon descent to an inner block, UNLESS
the same name in declared in the inner block. In the latter case, the
variable is held in abeyance while the machine is executing the inner
block, coming into force again when the end of the inner block is
reached.
Within any particular block the term local variable is used when
referring to variables declared in this block, and the term global
variables when referring to variables declared in any exterior block.
These points are illustrated by the following example.
(i) begin (ii) begin
real A real A
....... .......
A = 1 A = 1
begin begin
real A, B, C real B, C
............ .........
B = 1 B = 1
C = 4 C = 4
A = B+C A = B+C
end end
print (A,2,2) print (A,2,2)
end end
Here the name A refers to Here A is global to the inner
quite distinct variables block since this time A has
in the inner block and the not boon re-declared. In this
outer block. The print case the print instruction
instruction will print will print the value 5.
the value 1.
Notes (1) To communicate between blocks, global variables must be used,
since local variables are cancelled upon exit from a block.
(2) Labels and switch labels, unlike variables, are always local to
a block. It is thus impossible to enter a block except through the head of
the block (which is just as well as the local declarations are written
there). It is impossible to jump from one block to another.
(3) Similarly each repeat must be in the same block as the cycle
to which it refers.
58.
EXAMPLE OF A COMPLETE PROGRAM
Read in lists of positive integers and print them out with each
list sorted into increasing order of magnitude. Insert 2 blank lines
to separate one list from the next.
On input of data, each list will be headed by an integer giving
the number of elements in the list. After the last list, a single zero
will be fed in, indicating an imaginary list of zero length.

59. EXAMPLE OF A PROGRAM 0 begin 1 comment to arrange lists of positive integers in 2 comment increasing order of magnitude 3 integer p 4 1:read(p) 5 if p≤0 then stop 6 begin 7 integer i,j,AMAX,jMAX 8 integer array A(1:p) 9 cycle 1=1,1,p 10 read(A(i)) 11 repeat 12 -> 3 if p=1 13 cycle i=p,-1,2 14 AMAX=0 15 cycle j= 1,1,1 16 if AMAX ≥ A(j) then -> 2 17 AMAX= A(j) ; jMAX=j 18 2: repeat 19 A(jMAX)=A(i) 20 A(i)=AMAX 21 repeat 22 3: cycle i=1,1,p 23 newline 24 print(A(i),5,0) 25 repeat 26 end 27 newline 28 newline 29 -> 1 30 end of program
60.
Notes (1) p is declared in the outer block, but can still be used
in the inner block where it is a global variable. (Lines 8,9,12,13,22).
(2) The label 1 is in the outer block, so the instruction '-> 1'
must also be in the outer block.
(3) The line numbers given on the left are not printed with
a normal program, and should not appear on the program sheet, but the
compiler does in fact count physical lines in this way and will print
out the line number of any fault found in a program. In this connection,
note that a physical line may contain more than one declaration or
instruction, that is more than one 'line' as defined on Page 15.
(e.g. line 17).
(4) The sorting technique used in the above program has been
chosen because it is a convenient example. It is not an efficient
procedure and should not be used to sort large quantities of data.
A more efficient technique is given on Page 77.
62.
63.
ROUTINES AND FUNCTIONS
There are many occasions on which it is necessary to perform an
operation several times in different contexts within a program, or even
in different programs (perhaps written by different people). A
possible method of programming this operation as a unit is to write
it as a routine.
ROUTINES WITHOUT PARAMETERS
On page 55 we explained that a block can be regarded as one
compound instruction. Instead of writing out this block in full every
time it is required, we can give it a name which is then written
(as a single instruction) every time we wish the block to be carried out.
Such a named block is called a ROUTINE.
There are three operations involved in incorporating a routine
into a program (1) Declaration
(2) Calling
(3) Description
As an example, we use a routine to interchange the values of two
variables x and y.
(1) declaration meaning
routine spec interchange the name interchange is
to be the short title for a
routine (a block of
declarations and instructions)
which will be described
later.
(2) call meaning
interchange carry out the routine which
has the short title
interchange
(3) description meaning
routine interchange the routine interchange
integer z consists of the one
z = x declaration and three
x = y instructions given opposite.
y = z
end
64.
Notes (1) A routine description has the same structure as a
block except that begin is replaced by routine followed by its name.
(2) In the routine description given above, x and y are
global variables.
(3) The first line of the description is always the same
as the declaration, but with spec omitted.
(4) A routine may be called in any block interior to the
one in which it is declared (and described). In this way we can think
of local and global routines, in just the same way as local and global
variables.
(5) A routine call is an instruction and may be made
conditional:
e.g. if p ≠ 10 then interchange
(6) Normally, instructions in the routine are obeyed in
sequence until reaching end. If it is desired to stop the routine at
some other point, the instruction return may be used. This is
equivalent to a jump to end and hence cannot be used in an inner block
of the routine, return may be made conditonal.
Example Interchange x and y and square them if they are both positive.
routine interchange and square
integer z
z = x; x = y; y = z
if x≤0 or y≤0 then return
x = x*x; y = y*y
end
Note A second return could be written immediately before end, but would
be redundant.
65.
STRUCTURE OF BLOCKS CONTAINING ROUTINES
Routine descriptions are placed at the end of the block in which
they are declared. The general structure of a block can now be
extended to :-
begin
integer ...... )
real.......... ) declarations, including
routine spec interchange ) declarations of routines.
routine spec ....... )
........... ) instructions including
interchange ) routine calls.
........... )
routine interchange ) )
........ ) )
end ) ) routine descriptions, each
) having a block-like
routine ...... ) ) stucture of its own.
........ ) )
end ) )
end
66.
ROUTINES WITH PARAMETERS
The previously described routine 'interchange' will exchange the
values of x and y, but will be of no use if we wish to interchange any
other pair of variables.
In Atlas Autocode, to facilitate the use of the same routine in
different contexts within a program, the user is permitted to write the
routine using formal (or dummy) names for some or all of the variables
global to it. In each call of the routine, these formal names are replaced
by the appropriate actual names.
If formal names are used in the writing of a routine, then the
following modifications must be made to the procedures for declaring,
describing, and calling the routine.
(a) In declaring and in describing the routine its name must be
followed by a bracketed list of the formal parameters used, together with
a statement of their type.
(b) In calling the routine the name must be followed by a bracketed list
of the actual parameters which are to replace the formal parameters
on this occasion.
The designation 'parameter' has been used above in anticipation of
facilities which permit quantities other than names (for example elements
of arrays and arithmetic expressions) to be passed on to routines.
Example 1
integer a,b,i
integer array A(1:10)
routine spec interchange (integer name x,y) Declaration
.............
.............
interchange (a,b) Call 1
cycle i = 1,1,9
interchange (A(i) , A(10)) Call 2
repeat
.............
routine interchange (integer name x,y) Description
integer z
z = x; x = y; y = z
end
67.
Notes (1) Here x and y are the formal parameters.
(2) The actual parameters must be placed in the same order as the
formal parameters to which they correspond.
In call 1, x is replaced by a and y by b. In call 2, x is replaced by
A(1) and y by A(2).
(3) The statement of parameter type is omitted in calling the
routine, but the compiler checks to see that the actual parameters
listed are of the type indicated in the declaration.
PARAMETERS CALLED BY VALUE Parameter n in the example below
illustrates the use of a different type of formal parameter.
.............
integer shriek
routine spec FACT (integer name y, integer n)
.............
.............
FACT (shriek, 10)
.............
.............
routine FACT (integer name y, integer n)
integer i
y = 1
cycle i = 1,1,n
y = i*y
repeat
end
The difference between the formal parameter types
integer and integer name is important and must be carefully noted.
(a) integer name. When a routine call is made the first action
is to replace the formal integer name parameter at every
place where it occurs within the routine body by the
corresponding actual parameter given at the time of the call.
This must have been declared in the usual way either as an
integer variable or as an element of an integer array (see
the two routine calls in the example on page 66).
(b) integer In this case the first action is the declaration
of a variable of type integer local to the routine.
This variable is now filled with the value of the actual
parameter which may be any integer expression.
Note The integers n and i are both variables local to the
routine FACT. They are brought into existence upon entry to the
routine and their contents are lost upon exit. They differ in that
n has an initial value assigned, which varies from occasion to
occasion depending upon the value of the expression given as the
actual parameter on that occasion of call. In the call above, n
is initially set to 10.
68.
The parameter types real name and real are used in a similar manner.
The actual parameter corresponding to the parameter type real name must
have been declared as a real variable or as an element of an array. The
actual parameter corresponding to the parameter type real may be a general
(i.e. integer or real) arithmetic expression.
Parameters of type integer name and real name are said to be CALLED
BY NAME.
Parameters of type integer or real are said to be CAIXRD BY VALUE.
In Atlas Autocode parameters called by name are completely
determined by the actual values of all relevant quantities (including
global variables) of the time of call. For example it may happen that a
routine with a parameter list containing say
.........(real name x, integer name i, .......)
is called with the actual parameters
.........(A(j), j, ..........)
where A is the name of a previously declared real array. If the value of
j at the time of the call is, say, 10 then in the execution of the routine
the formal parameter x is replaced everywhere by A(10) no matter how
j varies.
The reader is warned that the alternative convention ( whereby, in the
above example, the array element replacing x would be determined by the
current value of j during the execution of the routine) is used in some
other programming languages ( e.g. Algol).
PASSING ON ARRAYS TO ROUTINES
A parameter of type real array name or integer array name is used in the
same manner as those of type real name and integer name. We can describe a
routine in terms of elements of an array with a formal (or dummy) name. In
each call, we give the actual name of the array which is to be used in
place of the dummy array on that particular occasion.
Example The following routine will double the first 10 elements of any
one-suffix array (provided it starts with suffix 1 and has at least 10
elements).
routine double (real array name X)
integer i
cycle i = 1,1,10
X(i) = 2X(i)
repeat
end
The routine is called by instructions such as:-
double (A)
double (B)
which will double A(1), A(2).....A(10) and B(1) .......B(10).
Note The routine and the two arrays would, of course, have been previously
declared in the usual manner.
69.
Example In the next example it is assumed that a number of square arrays
have been declared and a routine is required to print out certain sums
of consecutive diagonal elements such as A(5,5) + A(6,6) + ... +A(10,10).
routine trace (real array name X, integer m,n).
integer i
real z
z = 0
cycle i = m,1,n
z = z + X(i,i)
repeat
newline
print (z,5,5)
end
and instructions to call this routine might be
trace (A,5,10)
trace (B,1,50)
Note On all the Atlas Autocode compilers, there are four types of
parameters called by NAME:-
integer name
real name
integer array name
real array name
and two by value:-
integer
real
On the Manchester COMPILER AA only, there are two extra types called
by value:-
integer array
real array
For further details, see the appropriate reference manual. These
'array by value' facilities should be used with caution, not only
because of incompatability with other compilers, but also because they
can use large amounts of storage space and because of the time taken to
copy all the elements of a large array.
70.
FUNCTIONS
The function facilities are closely related to the routine facilites.
However, the result of a function call is a number (real or integer) and
function calls occur in arithmetic expressions. The declaration, call and
description of routines and functions are compared in the following table:-
Routine Function
Declaration routine spec.. a. real fn spec.......
b. integer fn spec ......
Result of call execution of a. real number
an instruction b. integer
Description routine .... a. real fn ...
b. integer fn ...
In place of return, the instruction result = is used to terminate the
evaluation of a function. However, the use of result is obligatory. Like
return, result must not occur in an inner block of a function.
Example The routine FACT can be rewritten as an integer function which
we rename FACT'
integer shriek
integer fn spec FACT' (integer n)
...............
shriek = FACT' (10)
...............
integer fn FACT' (integer n)
integer prod,i
if n = 1 then result = 1 ; comment see note 1 below
prod = 1
cycle i =. 2,1,n ; comment see note 1 below
prod = i* prod
repeat
result = prod
end
Note (1) the assignment of the value of the function to result. The
reader should study carefully the two occurrences of result :
depending on the value of n, either is a possible exit point. The
two lines marked with a comment could be combined as in the routine
FACT, but the similarity to the example to follow on page 77 would
be lost.
(2) Both the routine call FACT (shriek, 10) and the assignment
shriek = FACT' (10) produce identical results.
71.
Like routines, functions have the property of being global to any
block interior to the one in which they have been declared and described.
In particular, the functions listed on page 40 have the property of being
global to the user's program so that neither declaration nor description
is required,
Example
The specimen program for ordering lists of positive integers can be
rewritten to illustrate the use of the routine and function facilities.
A function MAX will be defined which finds the suffix of the largest
element in the list. In terms of these, the cycle which achieves the
ordering is written
cycle i = p,-1,2
j = MAX (A,i)
interchange (A(j), A(i))
repeat
with a considerable gain in legibility.
The full program is given on the next page.
Note (1) The integer array A is passed on to the function MAX in exactly
the same manner as was indicated previously for routines.
(2) The function MAX could have been written in terms of elements
of the global array A. To give the function a more general application,
we write it in terms of a (formal) array with name V. When calling
the function, we pass on the name A as the actual parameter to replace V.
(3) The instruction -> 1 in the outer block refers the label 1
of the outer block. The same instruction in the integer function MAX
refers to label 1 of that function.
72.
begin
comment to order lists of positive integers
integer p
1: read(p)
if p≤0 then stop
begin
integer i,j
integer array A(1:p)
integer fn spec MAX(integer array name V, integer k)
routine spec interchange (integer name a,b)
cycle i = 1,1,p
read (A(i))
repeat
-> 2 if p = 1
cycle i = p,-1,2
j = MAX(A,i)
interchange (A(j), A(i))
repeat
2: cycle i = 1,1,p
newline ; print (A(i),5,0)
repeat
integer fn MAX(integer array name V, integer k)
integer p,q,r
r = 0
cycle p = 1,1,k
if r ≥ V(p) then -> 1
r = V(P) ; q = p
1: repeat
result = q
end
routine interchange (integer name a,b)
integer z
z=a ; a=b ; b=z
end
end ; comment end of inner block
newlines (2) ; -> 1
end of program
73.
CHAPTER 7 : MORE ADVANCED FACILITIES
(NOTE Readers inexperienced in programming will probably
prefer to pass straight on to Chapter 8).
Routines and functions as parameters.
Example Numerical integration by trapezoidal rule.
Recursive use of routines and functions.
Examples (i) Calculation of factorials.
(ii) Quicksort.
(iii) The game of Hanoi.
Store mapping functions.
74.
75.
ROUTINES AND FUNCTIONS AS PARAMETERS
It is possible to include routines and functions among the formal
parameters of a routine or function by means of the type statements
routine, real fn, and integer fn. When calling the routine or function the
actual parameters must be the names of routines or functions declared
either at the head of the block in which the call is made or in any exterior
block. Note, however, that all quantities, other than the formal
parameters, used in a routine or function description must be global to
this description. It is not sufficient for them to be global at the time
of call.
Example
76.
begin
integer i
real fn spec TRAP SUM(real x1,x2, integer n, real fn f)
real fn spec circle(real x)
cycle i=10,10,50
newline
print(i,2,0); spaces(2)
print(TRAP SUM(0,1,i,circle),1,9)
repeat
real fn TRAP SUM(real x1,x2, integer n, real fn f)
real fn spec f(real y)
real h,SUM
integer i
h=(x2-x1)/n; SUM=f(x1)
cycle i=1,1,n-1
SUM=SUM+2f(x1+i*h)
repeat
SUM=SUM+f(x2)
result =h*SUM/2
end
real fn circle(real x)
result =sq rt(1-x²)
end
end of program
notes (1) The print-out from the program was:-
10 0.776129582
20 0.782116220
30 0.783610789
40 0.784236934
50 0.784567128
(slowly approaching the true value of 0.785398163).
(2) The formal function parameter f is declared a second
time on line 2 of routine TRAPSUM. This serves not as a declaration of
the name (this is made on the line above) but of the parameter list.
REMARK
There are certain difficulties in the use of functions and routines
as parameters in all the existing compilers. The user should consult
the appropriate reference manuals for further details.
77.
RECURSIVE USE OF ROUTINES AND FUNCTIONS
Routines and functions have the property of being global to any
block interior to the one in which they are declared. In particular,
a routine or function can be used within the description of that
routine or function itself. This process is called RECURSION.
Example A function RECFACT equivalent to the function FACT' of
page 00 can be defined recursively as follows:-
RECFACT(1) = 1
RECFACT(n) = n * RECFACT(n-1).
This is easily programmed:-
integer fn RECFACT (integer n)
if n = 1 then result = 1
result = n * RECFACT (n-1)
end
Example QUICKSORT. Quicksort is a method of sorting numbers (or any
other quantities) into order. It is generally far more efficient than
the techniques described earlier in this book. (For further details
of this method, see C. Hoare, The Computer Journal, April 1962)
The basic routine
(a) Selects some member of the set to be sorted, and uses
this as the 'partition bound'.
(b) Partitions the remainder of the set into two groups,
one containing members not greater than the partition
bound, and the other containing members not less than
it. These groups are positioned to the left and right
of the bound as in the diagram on the next page.
(c) Calls itself recursively to sort each of these two groups.
78. In the diagram and routine below, the partitioning bound, d, has been chosen arbitrarily to be the right-hand member.The partitioning is carried out as follows:- (a) Set pointers l and u to the lower and upper ends of the array to be sorted. (b) Dump the partitioning bound, leaving a location X(u) which can be over-written when required. (c) Move pointer l forward until we find a member > d. Put this member into location X(u), leaving X(l) free to be overwritten when required. (d) Move pointer u backwards until we find a member < d. Put this into X(l) ........ ........ (e) Steps (c) and (d) are continued alternately until pointers l and u meet. The bound, d, is then placed in X(u).
79.
A possible description of this routine is:-
routine real, quicksort(real array name X, integer a,b)
comment sorts elements of real array X from X(a) to X(b)
integer l,u
real d
return if a ≥ b
l=a ; u=b ; | set pointers
d=X(u) ; | dump partition bound
-> 2
1: l=l+1 ; | this section moves
-> 4 if l= u ; | l forward until
2: -> 1 unless X(1) > d ; | we find a member > d
X(u) = X(l)
3: u=u-1 ; | this section moves
-> 4 if l = u ; | u back until we
-> 3 unless X(u)<d ; | find a member < d
X(l)=X(u)
-> 1
4: X(u)=d ; | partitioning complete
real quicksort(X,a,l-1) ; | sort from X(a) to X(l-1)
real quicksort(X,u+1,b) ; | sort from X(u+1) to X(b)
end
Note Although, as we have seen, our first example of recursion can
equally easily be written using a cycle, this is not true of quicksort.
80.
Example The game of HANOI.
This is another example where recursion greatly simplifies the
writing of a program.
In this game one is given three pegs, and on one of these pegs
are a number of circular discs of different sizes, graded so that the
largest is at the bottom and the smallest at the top. The aim of the
game is to transfer the discs to one of the other pegs (making use of
the third as required) in such a way that there is never a larger disc
on a smaller one. Only one disc at a time may be moved.
If the solution to the game for (n-1) discs is known, then the
solution for n can readily be obtained. Let the pegs be numbered
1, 2 and 3, and let it be required that the n discs on 1 be transferred
to 3. This can be done by transferring the first (n-1) to 2, the last
to 3, and then the first (n-1) from 2 to 3. In the following program
n is the number of discs which have to be moved from peg i to peg j.
PROGRAM FOR GAME OF HANOI
begin
integer n,i,j
routine spec hanoi (integer m,p,q)
read (n,i,j)
hanoi (n,i,j)
routine hanoi (integer m,p,q)
if m=0 then return
hanoi (m-1,p,6-p-q) ; | if p,q are two pegs, other is 6-p-q
newline
print (p,1,0); caption s -> s ; print (q,1,0)
hanoi (m-1,6-p-q,q)
end
end of program
The output for the case n=2,i=1,j=3 is:-
1 -> 2
1 -> 3
2 -> 3
81.
STORE MAPPING FUNCTIONS
The store mapping function provides the user with the possibility
of renaming storage locations which have previously been named by a
declaration of type real array or integer array. The method of use of
a mapping function is almost identical to that of a function. For
example it is declared either by real map spec or integer map spec
depending on the nature of the variables to be renamed.
Like integer and real functions, mapping functions can appear in
arithmetic expression. However as the result of the store map is a
variable, it can also be written on the left hand side of an assignment.
Example
real x
real map spec W(integer i,j)
..............
X = W(2,3)
W(1,2) = 1 + x ↑ 3
..............
Note This illustrates the use of the store map both on the left and
on the right hand sides of an assignment.
The description of the store mapping function has the form
real map W(integer i,j,.....)
result = addr (A(integer expression, integer expression,..))
end
Notes (1) A is the name of the array to be renamed.
(2) Here it is assumed that A is global to the description of the
mapping function. However A could have been included in the
function heading as a formal parameter of type array name.
(3) There is no restriction on the number of suffices that can be
associated with either A or W.
(4) The integer expressions that determine the values of the
suffices of the array A can be general integer expressions
involving the formal parameters i,j,..... .
Example
real array A(1:1000)
real map spec W(integer i)
.............
real map W(integer i)
result = addr (A (i*i))
end
82.
Note In the example W(i) and A(i*i) are equivalent. For example W(10)
and A(100) are both valid titles for the same storage location.
Store maps have the great advantage that they permit economical
use of storage on a computer. For example if a two dimensional array is
symmetric (so that X(i,j) = X(j,i)) then it is completely specified by
the values X(i,j) with i ≥ j. It is therefore necessary to store only
this (lower) triangular array with a saving in storage space of nearly
50 per cent. An appropriate description of the mapping function might
be
real map X (integer i, j)
result = addr (A(i*(i - 1)/2 + j)) if i ≥ j
result = addr (A(j*(j - 1)/2 + i))
end
Note The saving in storage space gained by using mapping functions is
obtained by sacrificing speed in the execution of the compiled program.
For this reason mapping functions are not recommended for general use.
84.
85.
INPUT AND OUTPUT
Input and output of numbers and symbols is achieved by permanent
routines whose descriptions are held in the machine. These routines
are global to the whole program and may therefore be called without
further declaration and description. Although some of these routines have
already been explained, they are included here for the sake of completeness.
INPUT OF NUMBERS
read (a) Read the next number on the data tape into location a,
and move the tape on, ready for the next number.
(Parameter called by name).
read (a,b,c,d) Read the next four numbers into a,b,c and d respectively.
There is no limit to the number of parameters allowed
and each one may be either real or integer, or an element
of either an array or an integer array.
Notes (1) Although spaces in a program are disregarded, this
is not true on a data tape, where spaces can be used to
separate numbers from one another. Numbers written in
floating point form (Page 37) may have spaces between
! and the exponent, but in all other cases a space or
a newline character indicates the end of a number.
(2) In the case of the instruction read (i,x(i)), the
first number is assigned to i. The second number is then
read into x(i) where i takes the value just assigned.
86.
OUTPUT OF NUMBERS
print ((a+b+c)/n, i+1, j) Print out the value of the first expression
with (i+1) figures before and j figures
after the decimal point. If the expression
works out to contain less than (i+1) figures
before the decimal point, extra spaces will be
inserted. If it has more, the extra figures
will be printed, but the vertical alignment of
a column of results will be spoilt.
Parameters are called by VALUE, and so
may be expressions. The last two must be
integer expressions.
print fl ((a+b+c)/n,j) Print out the value of the first
expression in floating point form. One
figure is printed before and j after the
decimal point, additional powers of 10
being indicated by the symbol !, as on
Page 37.
Note. When using the print and print fl routines, a negative number is
preceded by - and a positive number by a space (to give correct vertical
alignment of a column).
QUERY PRINTING
On occasions it is convenient to print out the result of some
intermediate calculation. For example, this is often a help in locating
programming errors. A simple method of doing this is 'query printing'.
If an assignment to any variable (but not to result in a function) is
followed by a question mark e.g.
a = b + c ?
the effect is
(i) if a is real a = b + c ; print fl(a,10)
(ii) if a is integer a = b + c ; print(a,1,0)
Notes (1) In the case of the Edinburgh compiler, newline is
inserted before the printing instruction.
(2) The 'line' ignore queries added immediately before
the first begin of the program cancels query printing when it is
no longer required.
87.
INPUT OF SYMBOLS
read symbol(a) Read the next symbol on the data tape and
place it in location a. Move the data
tape on by one symbol.
Note (1). This routine can only read one
symbol at a time, unlike the read routine
which can have any number of parameters.
Note (2). a must be an integer variable
or an element of an integer array.
skip symbol Move the data tape on one symbol, without
reading anything into the machine.
a = next symbol Read the next symbol into integer location
a, without moving the data tape. (So the
same symbol can be read in a second time)
Note next symbol is a permanent integer
function, and can thus be used in integer
expressions and conditions.
For example:-
-> 7 if next symbol = '*'
REMEMBER When reading symbols, both spaces and newlines count as
symbols, whereas, when reading numerical data they simply mark the
end of a number.
OUTPUT OF SYMBOLS
caption......... )
print symbol( ) ) Have already been adequately
space, spaces ) discussed on Pages 19 and 31.
newline, newlines )
88.
CONDITIONAL INSTRUCTIONS
It is convenient to collect together a list of all types
of instruction which can be made conditional (by means of an if or
an unless clause).
Type Example with condition
(a) Assignment instructions a=b+c² if x=0
(b) Jump instructions ->7 if x ≠ 1
->Sw(i) unless j = 3
(c) Routine calls (including interchange(a,b) if a > b
permanent routines) print(a,1,0) unless a = 0
(d) caption......... if x ≠ 0 then caption O.K.
(e) result = ....... if a ≥ b then result = 17
(f) stop, return stop if n < 0 or m = 2
return if i = '*'
Notes (1) cycle..... , and repeat do not appear on the list.
They are not Instructions, but Separators (see classification
on page 15).
(2) The if or unless clause has the same effect whether
written before or after the instruction, except in the case of
caption ...... If the example at (d) above had been written
caption O.K. if x ≠ 0
the if clause would have been treated as part of the text of the
caption, giving an output, irrespective of the value of x:-
O.K.ifx≠0
89.
LIBRARY ROUTINES
Routines to carry out many of the standard computational processes
have been written in Atlas Autocode. Using these within one's own
program saves considerable programming effort. The reader should obtain
details from his Computer Unit.
EFFICIENCY
We give below some suggestions which may assist the reader to
write his programs in a form which will make efficient use of machine
time. He should, however, keep a sense of proportion, remembering that
his own time is also valuable and that the first objective should be to
make his program work successfully.
(1). The parts of a program in which efficiency is important are
those which are executed many times. For example, any minor improvement
made in the area (A) below will cause a saving on each of the 10,000
times this section is executed.
cycle i=1,10,100
cycle j=1,10,100
................ )
................ ) (A)
................ )
repeat
repeat
(2). Division takes longer than multiplication, so that 0.1*x
is computed more quickly than x/10.
(3). Whenever some part of an expression is required many
times, it should be evaluated once and stored, as in the right-hand
version below.
d=x*π/180
cycle i=1,1,100 cycle i=1,1,100
A(i)=A(i)*x*π/180 A(i)=A(i)*d
repeat repeat
(4). It takes longer to move numbers in and out of array elements
than simple variables. Again, the right-hand version below is the
more efficient.
X(i,j)=0 d=0
cycle k=1,1,15 cycle k=1,1,15
X(i,j)=X(i,j) + Y(k) d=d +Y(k)
repeat repeat
X(i,j)=d
90.
(5). It is far quicker to calculate numbers inside the
machine than to read data in or print answers out. Given some
reading taken during an experiment every 1/10 sec
time reading
12.0 2.137
12.1 3.657
12.2 6.678
..... .....
..... .....
..... .....
59.9 7.547
60.0 2.652
it is wasteful to read in the left-hand column at all. We can
read the first and last times (12.0 and 60.0), together with the
interval (0,1) and compute the intervening times.
Similarly, output should be reduced to the minimum that
the programmer really wishes to read. Apart from the saving of
machine time and money, the computer can disregard all
uninteresting results (which have to be adequately defined) far
more quickly than we can tear up unwanted sheets of paper and
assign them to the waste paper basket.
(6). When available, a Line Printer is a more efficient
method of output than punched paper tape. With the Line Printer,
answers should be printed right across the page, as the cost is
proportional to the number of lines printed. (A line of output is
limited to 120 characters).
(7). When fault finding, use 'query printing' with discretion.
Query printing within program loops is a common cause of large
quantities of output which are never read.
CHECKING OF PROGRAMS
The need for checking of programs cannot be overemphasised.
A check sheet to assist the reader to avoid-some of-the more common
errors is given on the next page.
91.
PROGRAM CHECK SHEET
1. General details Are all the special words of the language
correctly underlined ?
2. Have I a corresponding number of
(a) begin / end (also routine..../ end, etc) ?
(b) cycle / repeat (and at corresponding levels) ?
3. Declarations (a) Have I used the same name before at this level ?
(b) Have I got my commas and colons correctly
written in my array declarations ?
(c) Have I assigned values to the variables used
in the calculation of array bounds ?
4. Names Have they been declared (at an appropriate level) ?
5. Labels Have they been used before at this level ?
6. Jump instructions Has the label been set at this level ? If a
switch label, has it also been declared (at this level) ?
7. Expressions (a) Do left and right brackets correspond ?
(b) Have I any real quantities or functions being
assigned to integer variables or used as an exponent ?
(c) Can the expression got too large at any
intermediate stage or in the final value ?
8. Array elements Are the suffices all integer expressions, and
CAN THEY EVER TAKE VALUES OUTSIDE THE DECLARED BOUNDS ?
9. Cycles (a) Is the control variable an integer ?
(b) Are the 3 expressions all integer expressions ?
(c) Is expr(3)-expr(1) a non-negative multiple of expr(2) ?
10. Routine and function calls Has the routine/function been
declared and described at an appropriate level, and are the
actual parameters of legitimate type and correct in number ?
11. Functions Have I given a result ?
12. Division (a) Am I sure the denominator can never be zero or
dangerously close to zero ?
(b) In integer expressions on KDF 9, will all
intermediate results be integral ?
13. Square Roots Can the argument ever be negative ?
14. Logarithms Can the argument ever be negative or dangerously small ?
15. Stopping Have I arranged for the program to stop ?
16. General (a) Have I supplied a valid Job Heading ?
(b) Have I supplied data, and the right amount ?
92.
INDEX 93.
Arrays 17 Integer expressions 41
Dynamic array bounds 55(3a)
Array-name parameters 68 Integer variables 16
Multi-suffix arrays 49
Job heading 9
Arithmetic expressions,
see 'Expressions' Jump instructions 22
Blocks 21,55 Labels 22
with Routines 65 Switch labels 48
caption 19,31 Library routines 89
Comments 20 Line printer 7
Compiler 6,9(1) 'Lines' 15
Computers: basic operations 5 Local variables 57
Conditions 23,30,88 Mapping functions 81
Constants 37 Names 15
Cycles 43 Newlines 19,31
Data 9 Operators, precedence of 39
Declarations 16 Parameters of routines 66
of Arrays 17 Called by name 68,69
Of Routines 63 Called by value 68,69
Routines & fns as parameters 75
Efficiency 89
Query printing 86
Examples of programs
Average of numbers 24,46 Real expressions 41
Counting symbols 33,47
Examination results 49 Real variables 16
Function-type parameter 75
Hanoi 80 Recursion 77
Ordering of integers 58,71
Quicksort 77 result 70
Expressions 37 return 64
Functions 40
Integer or real 41 Routines
Precedence of operators 39 Library 89
Recursive use 77
Floating point constants 37 With parameters 66
Without parameters 63
Flow diagram 3
Separators 20
Functions
Defined by Programmer 70 Spaces 19,31
Mapping functions 81
Permanent 40 Symbols
Assignment of 30
Global variables 57 Conditions 30
Correspondence to integers 32
Hanoi, game of 80 Input 29,87
Output 31
Input 18,29,85,87
Order of program & data 9 Switch labels 48
Instructions Underlining 16
Assignment 18,30,42
Conditional 23,88 Variables 16
Input 18,29,85,87 Integer 16
Output 19,31,86 Local and Global 57
Real 16